In a previous post, I explored ingredient lists from dessert recipes from the website taste.com.au. In this post, I’ll be using that dataset to identify ingredients that influence a recipe’s rating (whether negatively or positively).
As a reminder, my main questions are:
- How well does ingredient composition predict the rating of a recipe?
- Which individual ingredients contribute to high and low scores?
- Which combinations of ingredients contribute to high and low scores?
- Can we use all of this to identify less common but promising combinations of ingredients?
To determine if a recipe’s rating can be predicted based on ingredient composition, I’ll be using linear regression. Though there are other approaches one could use, I care more about the interpretability of my model than how well it actually performs (though of course, a model that performs very poorly also won’t have much explanatory value).
However, there are a few possible problems with this approach that must be kept in mind. Firstly, a recipe is clearly much more than the sum of its ingredients. Other aspects of a recipe that contribute to its quality won’t be captured well using this approach. Also, in treating user-provided ratings as a measure of recipe quality I’m assuming that these ratings are a fair metric for how good a dish is.
With these caveats in mind, I’ll walk you through preparing the dataset for modelling and then making and checking some models.
Choosing the response variable
Since I want to figure out which ingredients contribute to high ratings, I could simply use the rating for a recipe as the response variable (the variable I’m trying to predict). There are two reasons why this could be a bad idea. Firstly, the ratings are on a 0-100 scale, but in principle there’s nothing to prevent a model using rating as a response variable from predicting values outside this range. Secondly, I know from the previous post that the ratings are very skewed, with many recipes having very high ratings. This means it will be hard to predict lower ratings.
For these reasons, I transformed the rating (using \(log(101 - rating)\)) to give me a less skewed distribution. You can see this in the plots below. The left plot shows the distribution of untransformed ratings and the right plot shows the distribution of transformed ratings.
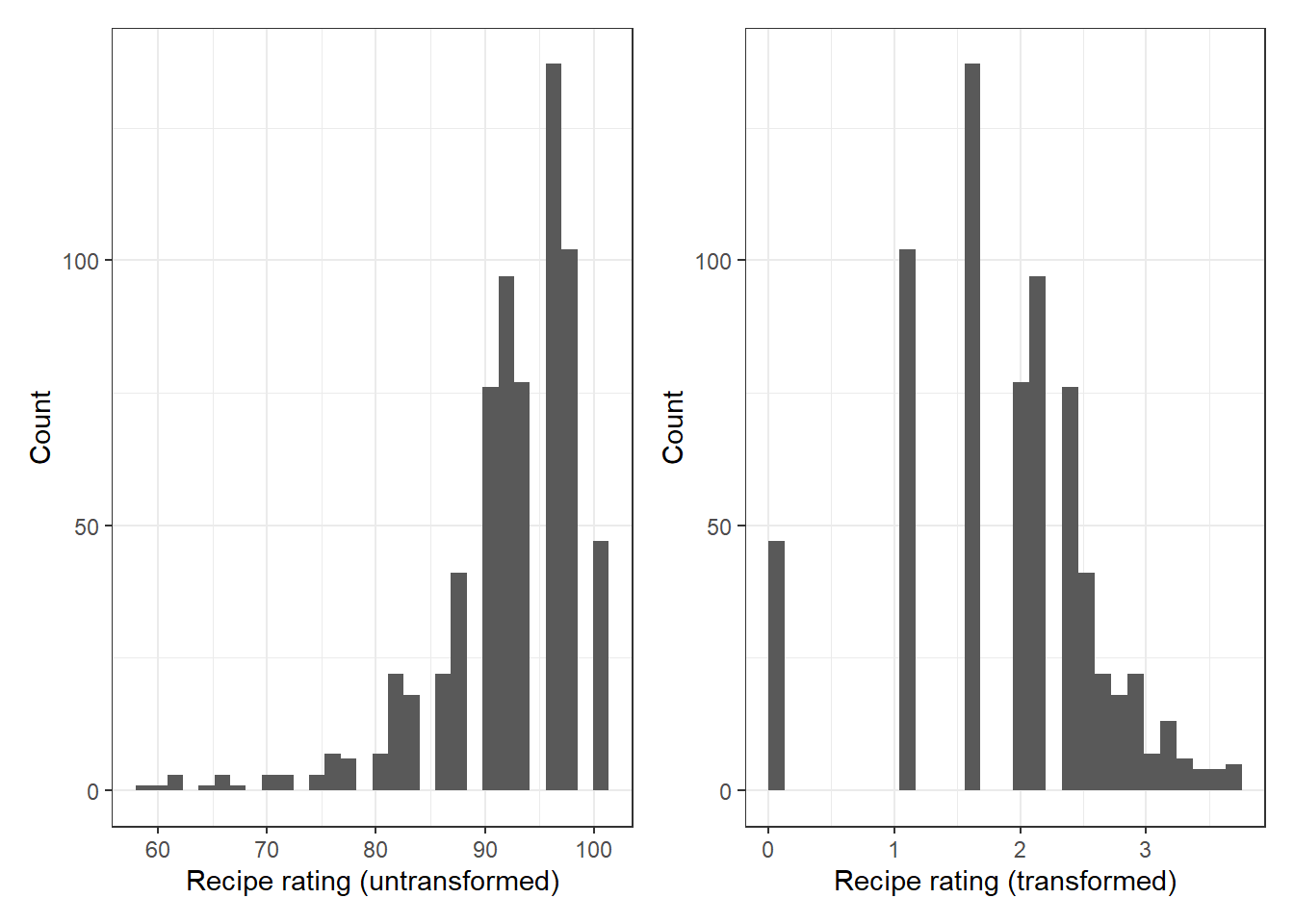
This transformation also effectively caps predictions at 100, which prevents impossibly high predictions. In principle it’s still possible to predict negative values, but because the lowest rating in this dataset is only 58, this likely won’t be a problem in practice. The downside of transforming the response variable is that it will make interpreting the coefficients from my models slightly less straightforward.
Preparing the data for modeling
You can read more about the steps I took to clean the dataset in the previous post. This included filtering out uncommon ingredients, since it will be hard to draw conclusions from about ingredients that appear in a small number of recipes. Also, uncommon ingredients are probably more likely to be substituted out which makes ratings of recipes including them less reliable. I also filtered out recipes with a small number of ratings. Because this dataset includes some recipes with the same name and similar ingredient lists (such as tiramisu and mud cake), I decided to keep only one recipe with each unique name. This left me with 678 recipes and 64 ingredients.
For modelling, I’ve created dummy variables for each of the ingredients (with 1 indicating it’s present in a recipe and 0 indicating it’s absent). The final dataset I’ll using for modelling has one row per recipe, with a column for each ingredient and a column for the transformed rating.
Checking for collinearity
One potential problem in linear regression is collinearity: having predictors that are highly correlated with each other. We can do a quick check for this using corrplot.
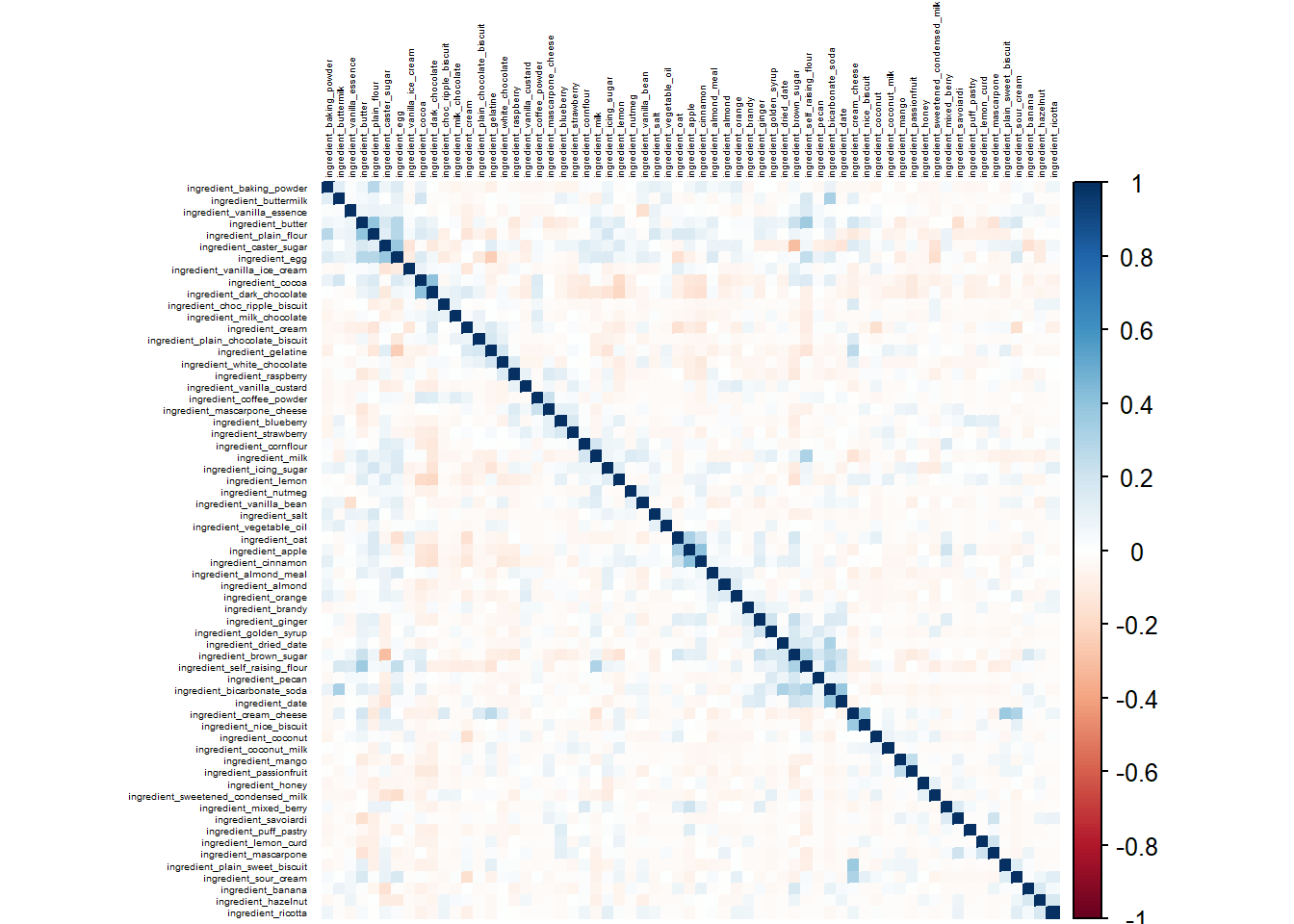
We do have some moderately high correlations here (like dark chocolate and cocoa, and apple and cinnamon). I won’t worry about these for now, but this is something to keep in mind if we run into problems later.
Beginning with a simple model
To begin with, we’ll use lm to fit a linear model with all the predictors (that is, every ingredient). It’s unlikely that every ingredient will actually significantly influence the rating, but this gives us a starting point for improving the model.
I fit models using both the untransformed and transformed rating as a response variable to confirm that this transformation is helpful. Indeed, the adjusted \(R^2\) value is better in the model using the transformed rating (0.18 versus 0.14). This is a useful metric because it tells us how well a model explains the variation in the response variable. In both cases the adjusted \(R^2\) is quite low, but this isn’t surprising given that we would expect the success of a recipe to be influenced by many factors other than the individual ingredients it contains.
Comparing the predictions from both models, we can see that the model that uses the transformed response variable does seem to be doing slightly better (the diagonal line shows where the points would fall if the model perfectly predicted ratings):
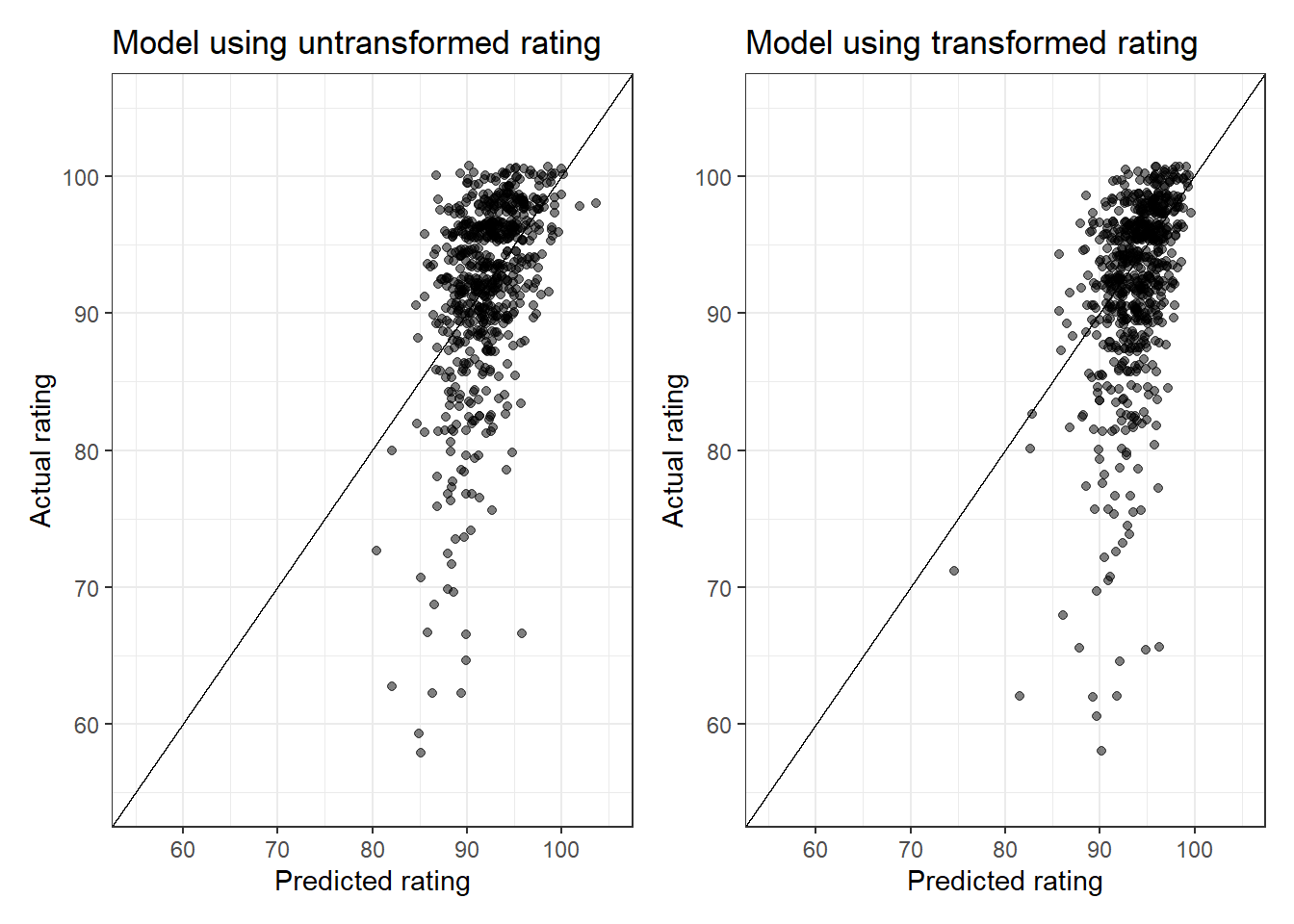
From the above plots, the range of values predicted using the transformed rating is closer to those seen in the data than those predicted using the first model are. However, both models do quite poorly when it comes to recipes that have a low rating; we see a lot of points falling well below the line where the actual rating is < 85.
Interestingly, the recipes that that the model makes poor predictions for are generally those with lower ratings. There are 56 recipes that have a predicted rating that is at least 10 points different from the actual rating, and these recipes have on average 13.2 ratings. This is a lot lower than the average of 25.4 ratings for recipes that had predicted ratings within 10 points of the actual rating. It’s possible that the average rating is a less reliable metric for recipes with fewer total ratings, which would explain why the model does a poorer job with those.
In these first models I included all ingredients as predictors, even though I expect that not all ingredients will contribute to a recipe’s rating. Looking at the summary we can see that it is true that very few of these predictors are significant:
##
## Call:
## lm(formula = response ~ ., data = dt_recipes_model[, -c("recipe_id",
## "recipe_name", "no_ratings", "rating")])
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.26170 -0.40197 0.01344 0.47234 2.01347
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.497548 0.094886 15.783 < 2e-16 ***
## ingredient_almond -0.322747 0.134189 -2.405 0.01646 *
## ingredient_almond_meal -0.255371 0.119440 -2.138 0.03291 *
## ingredient_apple 0.081315 0.142717 0.570 0.56905
## ingredient_baking_powder -0.050997 0.119200 -0.428 0.66893
## ingredient_banana -0.049847 0.167078 -0.298 0.76554
## ingredient_bicarbonate_soda -0.388211 0.158463 -2.450 0.01457 *
## ingredient_blueberry -0.175700 0.161144 -1.090 0.27600
## ingredient_brandy 0.089669 0.199234 0.450 0.65282
## ingredient_brown_sugar -0.048166 0.092744 -0.519 0.60371
## ingredient_butter 0.101026 0.079187 1.276 0.20251
## ingredient_buttermilk 0.052238 0.225027 0.232 0.81651
## ingredient_caster_sugar 0.061195 0.078710 0.777 0.43718
## ingredient_choc_ripple_biscuit -0.247687 0.224153 -1.105 0.26960
## ingredient_cinnamon 0.035450 0.107274 0.330 0.74117
## ingredient_cocoa 0.092602 0.085947 1.077 0.28171
## ingredient_coconut -0.010838 0.112927 -0.096 0.92357
## ingredient_coconut_milk 0.442547 0.218818 2.022 0.04356 *
## ingredient_coffee_powder -0.272050 0.196265 -1.386 0.16621
## ingredient_cornflour 0.193624 0.123556 1.567 0.11761
## ingredient_cream 0.012634 0.061700 0.205 0.83782
## ingredient_cream_cheese 0.132867 0.118524 1.121 0.26272
## ingredient_dark_chocolate 0.065510 0.079528 0.824 0.41042
## ingredient_date -0.151573 0.240652 -0.630 0.52903
## ingredient_dried_date -0.585233 0.251495 -2.327 0.02029 *
## ingredient_egg 0.328887 0.082188 4.002 7.06e-05 ***
## ingredient_gelatine 0.419355 0.130755 3.207 0.00141 **
## ingredient_ginger -0.479010 0.236159 -2.028 0.04296 *
## ingredient_golden_syrup 0.278107 0.156980 1.772 0.07696 .
## ingredient_hazelnut 0.412259 0.227299 1.814 0.07021 .
## ingredient_honey -0.155811 0.190530 -0.818 0.41380
## ingredient_icing_sugar 0.001625 0.068977 0.024 0.98121
## ingredient_lemon -0.044728 0.088708 -0.504 0.61429
## ingredient_lemon_curd 0.030237 0.244496 0.124 0.90162
## ingredient_mango -0.327772 0.233578 -1.403 0.16104
## ingredient_mascarpone 0.252304 0.190960 1.321 0.18691
## ingredient_mascarpone_cheese 0.082060 0.236666 0.347 0.72891
## ingredient_milk 0.111587 0.078944 1.413 0.15802
## ingredient_milk_chocolate 0.052375 0.153895 0.340 0.73373
## ingredient_mixed_berry -0.091742 0.196820 -0.466 0.64129
## ingredient_nice_biscuit -0.258181 0.237386 -1.088 0.27720
## ingredient_nutmeg 0.174521 0.221275 0.789 0.43059
## ingredient_oat 0.161366 0.212362 0.760 0.44763
## ingredient_orange 0.111358 0.132726 0.839 0.40179
## ingredient_passionfruit -0.166311 0.141536 -1.175 0.24043
## ingredient_pecan -0.106299 0.230632 -0.461 0.64503
## ingredient_plain_chocolate_biscuit -0.131138 0.215381 -0.609 0.54284
## ingredient_plain_flour 0.176530 0.079738 2.214 0.02720 *
## ingredient_plain_sweet_biscuit -0.200415 0.216896 -0.924 0.35584
## ingredient_puff_pastry -0.311944 0.199080 -1.567 0.11765
## ingredient_raspberry 0.081284 0.097397 0.835 0.40429
## ingredient_ricotta 0.195855 0.244599 0.801 0.42360
## ingredient_salt -0.104178 0.186899 -0.557 0.57745
## ingredient_savoiardi -0.277788 0.249976 -1.111 0.26689
## ingredient_self_raising_flour 0.081199 0.087924 0.924 0.35610
## ingredient_sour_cream -0.309124 0.135732 -2.277 0.02310 *
## ingredient_strawberry -0.145384 0.116082 -1.252 0.21089
## ingredient_sweetened_condensed_milk 0.260315 0.142478 1.827 0.06818 .
## ingredient_vanilla_bean -0.024012 0.071268 -0.337 0.73629
## ingredient_vanilla_custard -0.807239 0.189768 -4.254 2.43e-05 ***
## ingredient_vanilla_essence 0.090426 0.105109 0.860 0.38996
## ingredient_vanilla_ice_cream -0.484023 0.147350 -3.285 0.00108 **
## ingredient_vegetable_oil 0.346766 0.197594 1.755 0.07977 .
## ingredient_white_chocolate 0.055170 0.102369 0.539 0.59013
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7189 on 614 degrees of freedom
## Multiple R-squared: 0.2554, Adjusted R-squared: 0.179
## F-statistic: 3.343 on 63 and 614 DF, p-value: 1.23e-14Improving the model by removing predictors
The model does predict recipe rating to some extent, but it clearly includes many predictors that aren’t doing much. To simplify and improve the model, we will use MASS::stepAIC to pare down the model. stepAIC doesn’t a necessarily find the best possible subset of predictors because it doesn’t test all possible combinations, but it should certainly help in reducing the number of predictors while retaining those that improve the model.
The plot below shows the predictors that remain in the model selected by stepAIC as well as their coefficient estimates and confidence intervals (on the transformed scale). From the original list of 64 ingredients we are left with 26. In interpreting the plot, note that because we’re working with the transformed scale, an ingredient with a negative coefficient estimate is associated with higher ratings.
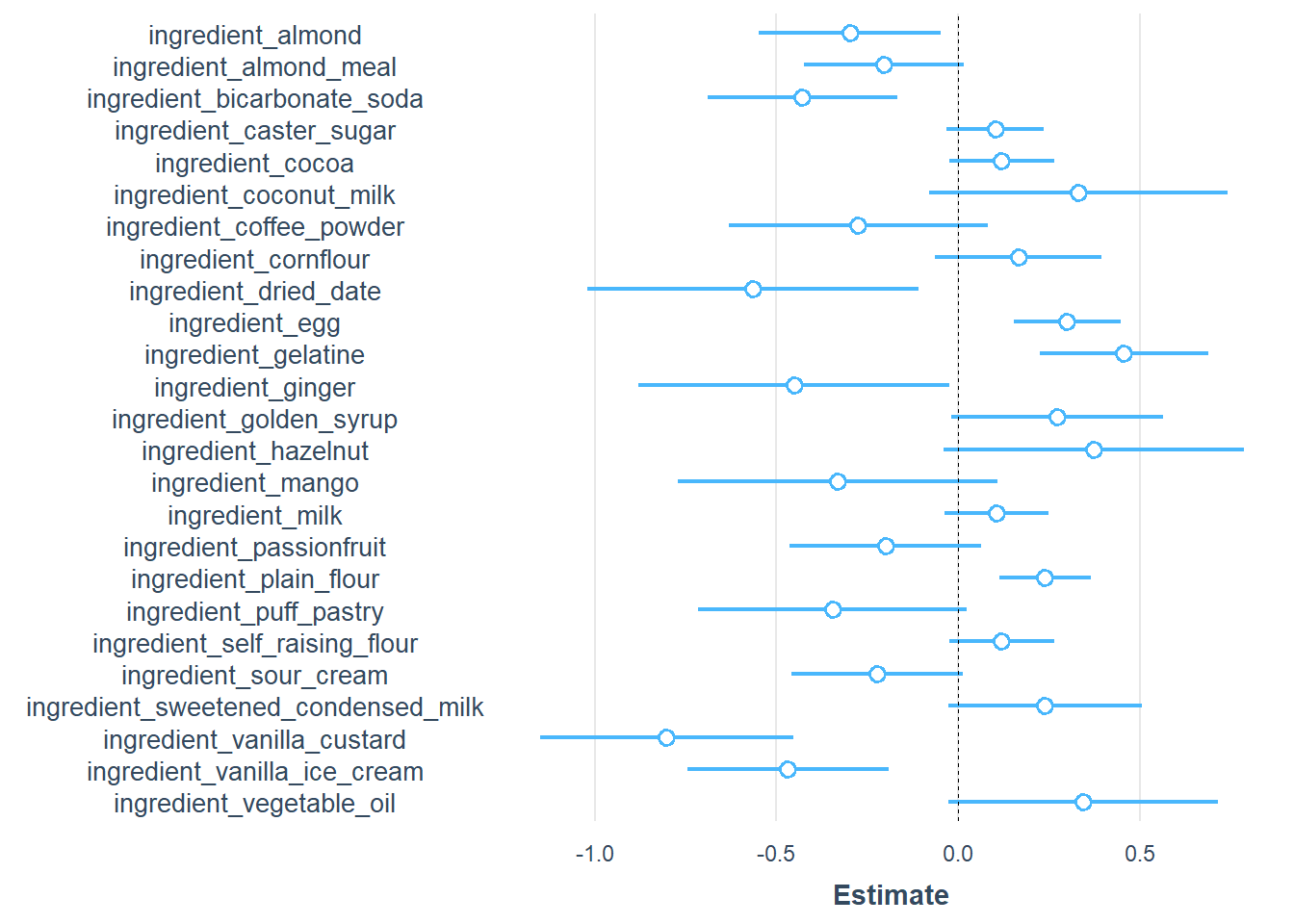
Many of the ingredients that remain in the model are what we might consider core ingredients, such as flour, eggs, and sugar. In these cases the estimates tend to be only modestly different from 0 but the confidence intervals are quite narrow (because there are a lot of recipes with these ingredients).
So what does this tell us about ingredients that positively or negatively affect recipe scores? Almond, dried date, ginger, mango, passionfruit, and vanilla custard are also associated with higher scores. Conversely, hazelnut and gelatine are associated with lower scores.
Let’s return to the original data to confirm this. The boxplots below show the range of ratings for recipes with and without each ingredient. The numbers in the boxes are the number of recipes in each category. You can see that in several cases there are not many recipes containing that ingredient, which means we should interpret those results more cautiously.
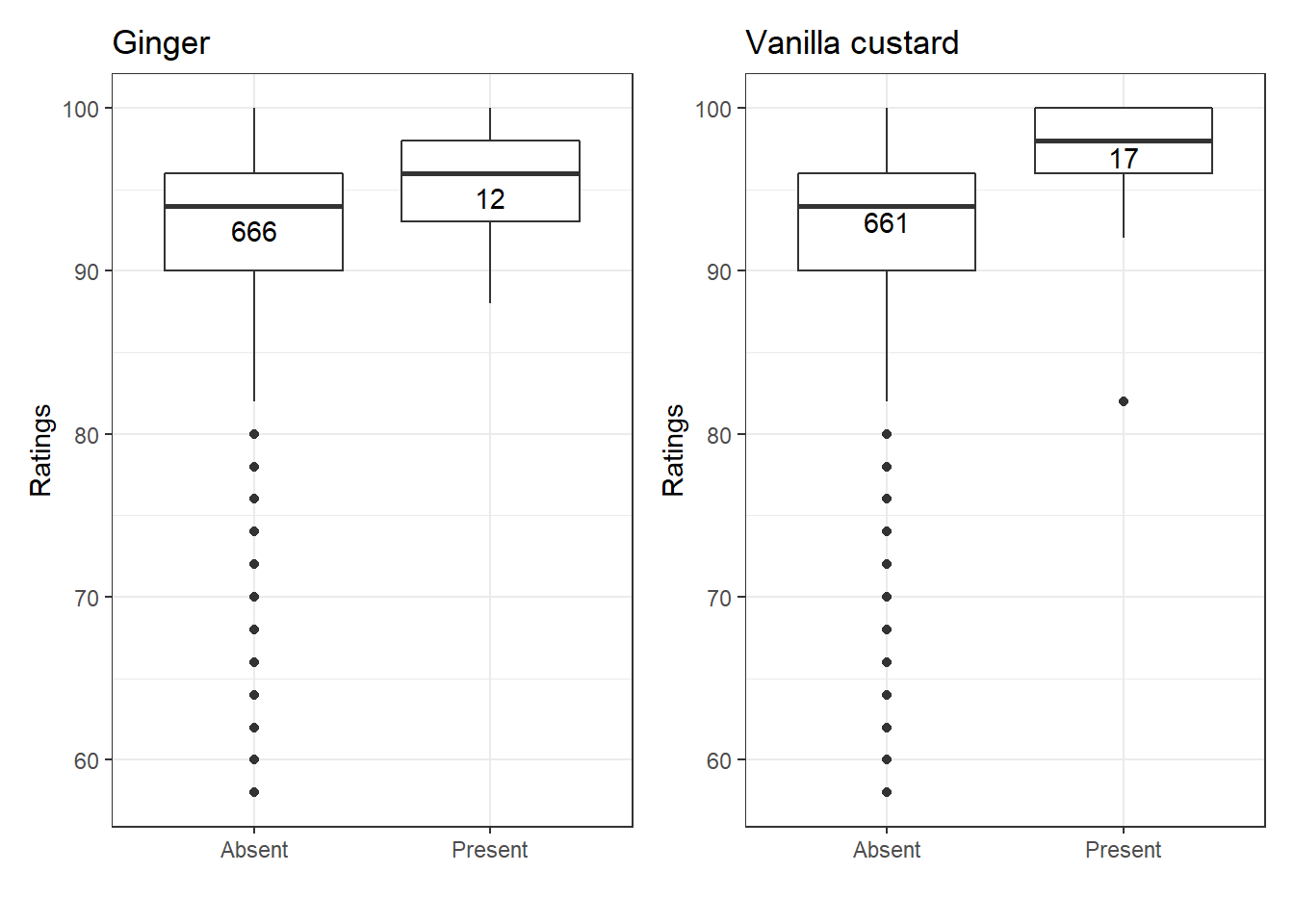
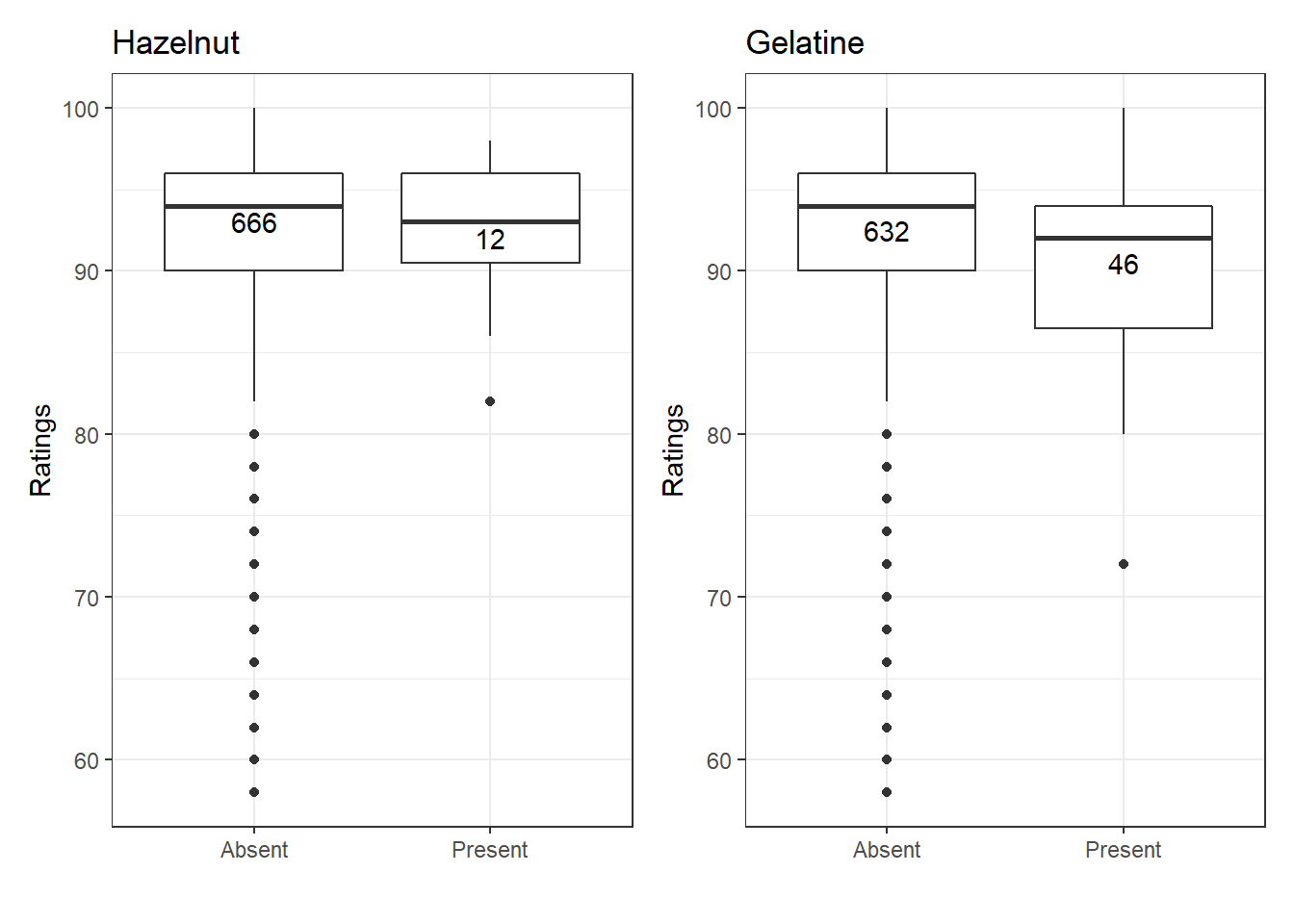
We see that recipes with vanilla custard or ginger have higher ratings than those without, consistent with our regression coefficients. On the other hand, recipes with hazelnut and gelatine get worse ratings in general than recipes without these ingredients.
Exploring ingredient combinations
One of the original goals was to try to find combinations of ingredients that contribute to high ratings. I’m particularly interested in is cases where a combination of two ingredients contributes more to a rating than you would expect simply based on the presence of both.
My original plan was to use interaction terms to try to capture this, but as it turns out the dataset I’m using here is too small to do this. However, there are still some simple ways to identify promising ingredient combinations. For each ingredient, we can generate a list of other ingredients that it is often combined with, how many recipes have each combination, and the average rating of recipes with that combination. Bear in mind that this won’t be terribly robust since the numbers of recipes is small.
Below are plots showing the ratings of recipes with each of two ingredients individually and in combination. The horizontal bars indicate the mean rating for recipes in each grouping.
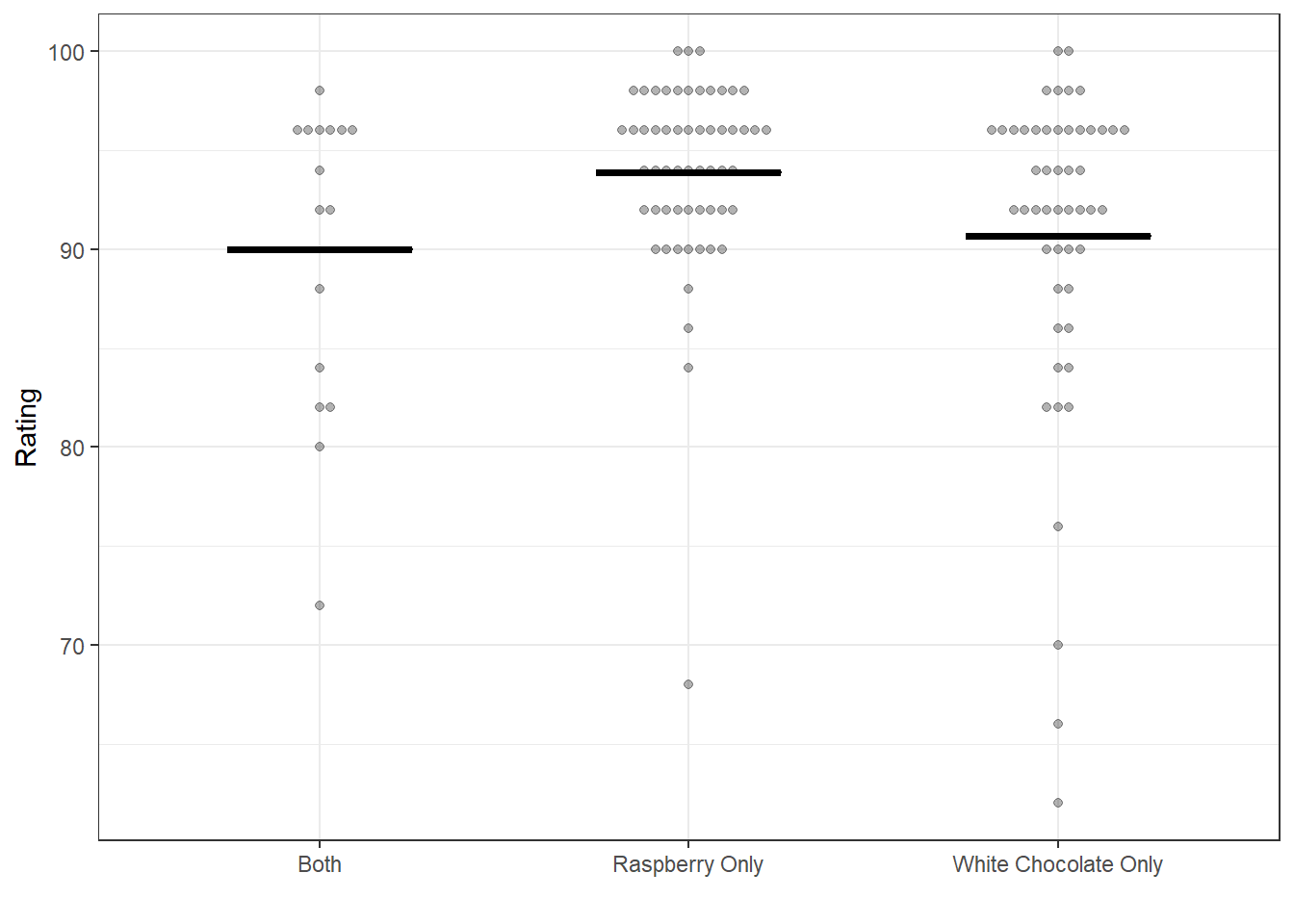
Raspberry and white chocolate is a fairly standard combination, so I was surprised to see that in this dataset recipes with raspberry and white chocolate have lower ratings that recipes with raspberry only (though similar to those with white chocolate alone).
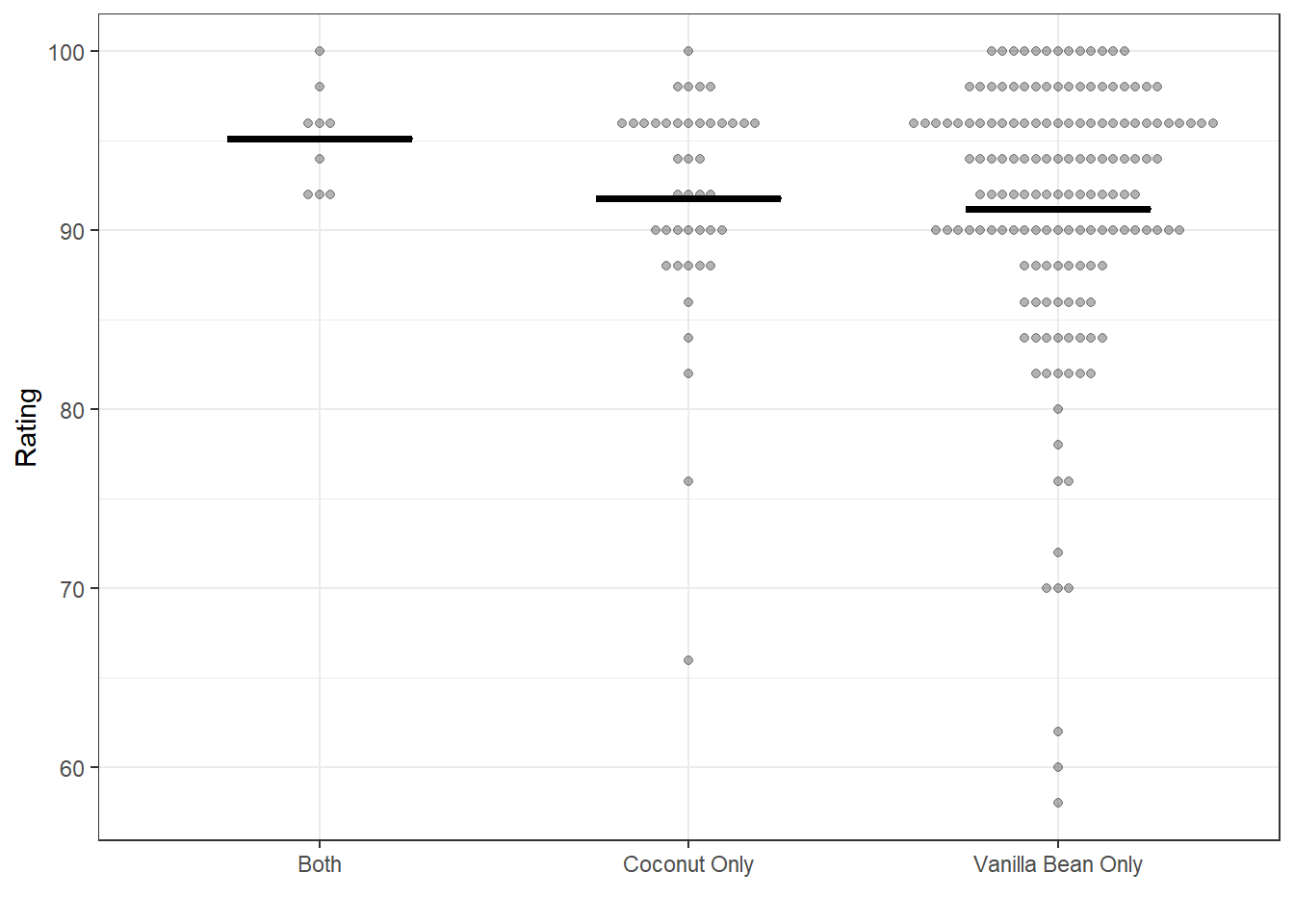
Conversely, recipes with both coconut and vanilla bean do better than those with only one of the two. While the number of recipes with both ingredients is small and thus we should interpret this cautiously, this suggests coconut and vanilla could be a good combination.
Summary
The main goal of this and the previous post was to determine if recipe rating could be predicted based on ingredient list alone, and if so, to identify ingredients contributing to high and low ratings. Despite some caveats with this approach, we were able to find a model that does accounts for some of the variation in ratings. This suggests that ingredient composition is an important influence on dessert recipe ratings, albeit amongst many other factors. The regression coefficients from our final model allowed us to identify some ingredients associated with high or low ratings in this dataset.
The size of the recipe dataset after filtering out rare ingredients and recipes with few ratings was a significant limitation here. This meant that it wasn’t possible to robustly identify synergistic combinations of ingredients as I’d originally intended. Nonetheless, this post shows that it is possible in principle to identify ingredients that may contribute to high and low recipe ratings. With a larger dataset it may be possible to extend this to identify interesting combinations of ingredients.